Spread of Infectious Disease
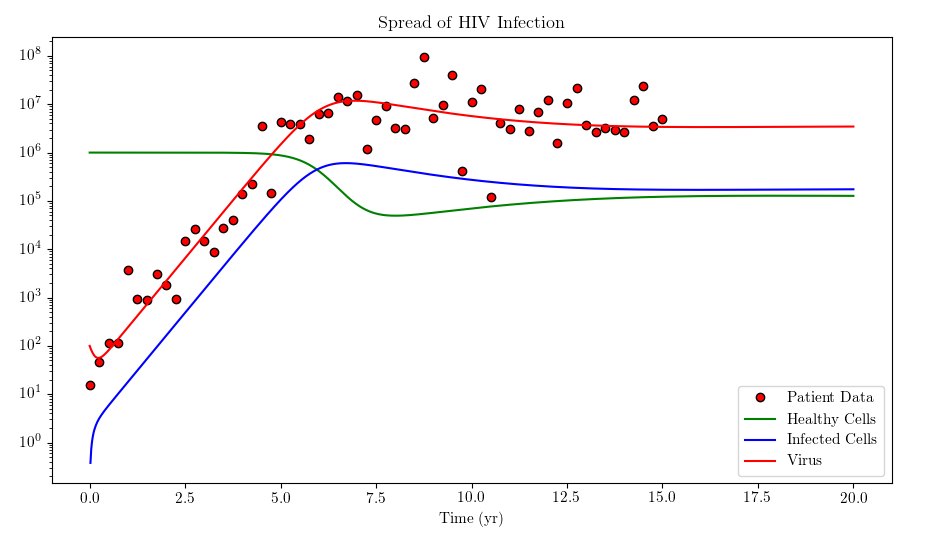
SIR(Susceptible, Infectious, Recovered) model is derived analytically and coupled differential equations are simultaneously solved using existing methods of SciPy and manual implementation of RK4. Stability of the disease is determined using symbolic methods from SymPy. Evolution of the disease within the society is visualized using Matplotlib. In the same manner, spread of HIV infection in the body is modelled and compared with publicly available data from an academic journal.

The system is governed by the following set of differential equations
\[\begin{align} \begin{aligned} \dfrac{\mathrm{d}S}{\mathrm{d}t} &= - \frac{\beta}{N}SI \\[3ex] \dfrac{\mathrm{d}I}{\mathrm{d}t} &= \frac{\beta}{N}SI - \gamma I \\[3ex] \dfrac{\mathrm{d}R}{\mathrm{d}t} &= \gamma I \\[1ex] \end{aligned} \end{align}\]where $\beta$ is the infection rate, $\gamma$ is the recovery rate, and $ N = S + I + R $ is the population size.
In the same manner, a model for spread of HIV infection in the body can be constructed. Numerical solutions of coupled differential equations are shown below: